INDUKSI MATEMATIKA (RAHMA FAUZIAH XI IPS 2)
Induksi vs Deduksi
By the way, emang kenapa sih kok metode seperti ini diberi nama Induksi Matematika? Apakah ada hubungannya dengan penalaran induktif dalam logika? Nah, sebenernya nggak ada hubungannya karena penalaran yang digunakan dalam Induksi Matematika ini justru penalaran deduktif, bukan penalaran induktif. Loh, kok gitu? Nah, supaya tahu kenapa begitu, kita coba pelajari dulu apa bedanya penalaran induktif dengan penalaran deduktif
Penalaran Induktif yang Beneran
Penalaran induktif yang beneran itu tidak ada hubungannya sama sekali dengan Induksi Matematika.
Sederhananya, penalaran induktif mengambil kesimpulan dari premis-premis umum (pengamatan, data, fakta) lalu kemudian mengambil kesimpulan yang bersifat spesifik (hipotesis).
Jadi, kesimpulan yang diambil dari penalaran induktif itu sifatnya tidak pasti, melainkan “mungkin benar”. Salah satu kecenderungan umum dari penalaran induktif itu adalah dia mengambil kesimpulan general dari berbagai kasus khusus. Contohnya begini:
Joni sering bepergian keliling dunia. Ketika dia ke Amerika, dia melihat seluruh angsa di sana warnanya putih. Ketika dia pergi ke Eropa, dia melihat seluruh angsa di sana warnanya putih juga. Ketika dia pergi ke Tiongkok, ternyata seluruh angsa di sana warnanya juga putih. Akhirnya dia berkesimpulan bahwa seluruh angsa di dunia ini warnanya putih.
Pada contoh di atas, Joni melakukan generalisasi dari berbagai kasus khusus yang dia lihat. Penalaran yang dilakukan Joni ini adalah penalaran induktif. Di sini elo bisa lihat bahwa penalaran semacam itu masih mungkin salah. Bahkan pada kasus ini, ya kesimpulannya memang salah. Kalau aja Joni sempet dateng ke Australia, dia akan melihat angsa yang berwarna hitam di sana. Jadi, kesimpulan bahwa seluruh angsa di dunia ini berwarna putih itu salah.
Terus, apakah argumen induksi ini tidak bisa dijadikan argumen yang kuat? Argumen induksi ini bisa merupakan argumen yang lemah (seperti contoh angsa di atas), bisa juga merupakan argumen yang kuat. Metode ilmiah yang kita gunakan di sains itu juga menggunakan penalaran induktif kok.
Contohnya di artikel Fanny yang membahas penelitian tentang rokok. Penelitian tersebut dilakukan kepada segelintir orang, tapi kita bisa mengambil kesimpulan secara general bahwa itu berlaku pada semua orang. Apakah kesimpulannya bisa salah? Bisa. Tapi kemungkinannya kecil karena penelitian semacam itu sudah diulang berkali-kali dengan berbagai konteks dan hasilnya sama.
Penalaran Deduktif
Nah, sekarang kita masuk ke penalaran deduktif. Penalaran deduktif merupakan pengambilan kesimpulan secara logis berdasarkan premis-premis yang ada.
Dari definisi ini jelas ya bahwa penalaran deduktif itu sifatnya pasti. Dalam penalaran deduktif, tidak ada generalisasi. Contoh penalaran deduktif itu seperti ini:
Premis 1: Semua orang akan mati
Premis 2: Socrates adalah orang
Kesimpulan: Socrates akan mati
Contoh di atas adalah contoh klasik penalaran deduktif. Jadi kalau premis 1 dan premis 2 itu benar, maka kesimpulannya juga sudah pasti benar juga. Kita lihat contoh lain yah.
Premis 1: Semua bebek kakinya tiga
Premis 2: Donal adalah bebek
Kesimpulan: Donal kakinya tiga
Nah, di sini kayaknya ada yang salah nih, kok Donal kakinya tiga. Bukannya dua? Apakah kesimpulan di atas itu benar? Well, gara-gara premisnya salah, kesimpulannya jadi salah juga. Tapi penalaran di atas itu adalah penalaran yang valid secara deduktif. Kenapa valid? Karena kalau kita asumsikan premis 1 itu benar, dan premis 2 itu benar juga, maka “Donal kakinya tiga” adalah kesimpulan yang valid, atau bahasa Indonesianya, kesimpulan yang sah.
Biar lebih jelas elo bisa lihat gambar di bawah ini, penalaran induktif menghasilkan kesimpulan yang kuat atau lemah. Sedangkan penalaran deduktif menghasilkan kesimpulan valid dan ga valid.
Induksi Matematika – Deduktif atau Induktif?
Sekarang kita kembali lagi ke Induksi Matematika. Jadi sebenarnya Induksi Matematika ini menggunakan penalaran induktif atau deduktif? Dari deskripsi di atas, jelas lah ya bahwa Induksi Matematika itu menggunakan penalaran deduktif. Karena seperti yang sudah disebutkan di atas, penalaran deduktif ini sifatnya pasti. Dia tidak menggunakan generalisasi dalam mengambil kesimpulan.
Ketika kita menyimpulkan bahwa rumus Sn itu berlaku untuk semua n bilangan asli, kesimpulan itu diambil bukan dengan mengambil sample beberapa nilai n. Kesimpulan itu diambil benar-benar dengan melakukan uji secara deduktif kepada seluruh nilai n yang berada dalam ruang lingkup rumus Sn tersebut.
PEMBUKTIAN INDUKSI MATEMATIKA
Induksi matematika digunakan untuk membuktikan suatu pernyataan untuk setiap bilangan asli. Untuk melakukan pembuktian menggunakan induksi matematika, ada langkah-langkahnya, nih. Bagaimana langkah-langkah melakukan induksi matematika?
Waduh, maksudnya apa tuh ya langkah-langkah di atas. Oke, biar nggak bingung, mending langsung aja kita aplikasikan ke contoh soal di bawah ini.
Buktikan deret 1 + 2 + 3 + ... + n = 1/2 n(n+1)
- Langkah pertama
Kita akan buktikan untuk n = 1 adalah benar. Karena pernyataan tersebut merupakan deret, maka n di sini maksudnya jumlah suku pertama deret tersebut. Nah, yang diminta n = 1, berarti jumlah suku pertamanya hanyalah 1. Kemudian, kita substitusi semua n dengan 1. Jadi,
Langkah pertama terbukti ya karena ruas kiri dan kanannya sama.
- Langkah kedua
Kita asumsikan pernyataan benar untuk n = k. Berarti jumlah suku pertamanya itu dari 1 + 2 + 3 + ... + k, ya. Sehingga,
Pernyataan tersebut kita asumsikan atau kita anggap benar. Kemudian, kita lanjut ke langkah ketiga.
- Langkah ketiga
Buktikan untuk pernyataan n = k + 1 juga benar. Kita bisa membuktikannya menggunakan modal dari langkah kedua. Karena kita mau n = k + 1, maka di ruas kiri, kita tambahkan satu suku, yaitu k + 1. Jadi,
Selanjutnya, kamu ingat nggak dengan sifat distribusi pada perkalian? Kalau ada (a + b)(c + d), maka bisa menjadi a(c + d) + b(c + d). Nah, di ruas kiri, bisa kita ubah persamaannya menggunakan sifat perkalian distribusi.
Misalnya, a = k, b = 2, dan (c + d) = (k + 1). Berarti,
DAFTAR PUSTAKA
judul postingan : INDUKSI MATEMATIKA
sumber materi : ruang guru (https://www.ruangguru.com/blog/matematika-kelas-11-pembuktian-matematika), zenius (https://www.zenius.net/blog/induksi-matematika)
tahun penulisan sumber materi : ruang guru (2022), zenius (2022)

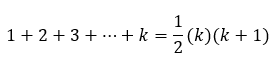

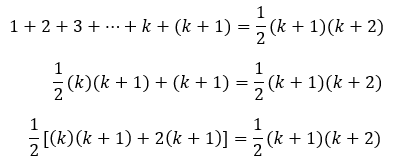


Komentar
Posting Komentar