PROGRAM LINEAR (RAHMA FAUZIAH XI IPS 2)

 Pertidaksamaan Linear Dua Variabel

Konsep persamaan dan sistem persamaan linear dua variabel sudah kamu pelajari. Prinsip yang ada pada sistem persamaan juga kita gunakan untuk menyelesaikan pertidaksamaan atau sistem pertidaksamaan linear dua variabel.

Prinsip yang dimaksud adalah menentukan nilai variabel yang memenuhi sistem pertidaksamaan linear tersebut.

Definisi

Pertidaksamaan linear dua variabel adalah pertidaksamaan yang berbentuk

ax + by + c < 0

ax + by + c ≤ 0

ax + by + c > 0

ax + by + c ≥ 0

dengan:

a, b : koefisien (a ≠ 0, b ≠ 0, a,b ∈ R)

c : konstanta (c ∈ R)

x, y : variabel (x, y ∈ R)

Contoh

Tentukan himpunan penyelesaian dan gambarkan grafik untuk setiap pertidaksamaan di bawah ini.

 –2x + y > 5, untuk x dan y semua bilangan real

Alternatif Penyelesaian

Dengan menguji nilai-nilai x dan y yang memenuhi – 2x + y > 5 , maka dapat ditemukan banyak pasangan x dan y yang memenuhi pertidaksamaan.

Ilustrasi himpunan penyelesaian, jika dikaji secara geometris disajikan pada gambar berikut.


Dari gambar diperoleh bahwa terdapat titik yang tak hingga banyaknya (daerah yang tidak diarsir) yang memenuhi –2x + y > 5.

Kali ini, melalui grafik, kita dapat memilih sembarang titik, misalnya titik (–5, 0), sedemikian sehingga –2(–5) + 0 = 10 > 5 adalah pernyataan benar.

Contoh Soal Program Linear dan Pembahasan

Tentukanlah sebuah nilai minimum dari: f(x, y) = 9x + y pada daerah yang telah dibatasi oleh 2 ≤ x ≤ 6, dan 0 ≤ y ≤ 8 serta x + y ≤ 7.Pembahasan 1:

  • Langkah 1 yakni menggambar grafiknya terlebih dahulu:


    • Langkah ke-2 menentukan titik-titik ekstrimnya:

    Maka berdasarkan gambar diatas, ada 4 titik ekstrim, yaitu: A, B, C, D dan himpunan penyelesaiannya ada di area yang telah diarsir.

    • Langkah yang ke-3, yakni menyelidiki nilai optimum:

    Berdasarkan grafik diatas dapat diketahui titik A dan B mempunyai nilai y = 0, sehingga kemungkinan menjadi nilai minimum.

    Selanjutnya kedua titik disubstitusikan kedalam f(x,y)=9x+y.untuk dibandingkan.



  • Dengan membandingkan tersebut,maka bisa disimpulkan bahwa titik A memiliki nilai minimum 18.

Contoh Soal 2:

Tentukanlah dimana nilai maksimum fungsi f(x, y) = 4x + 5y yang akan dicapai pada pada grafik ini!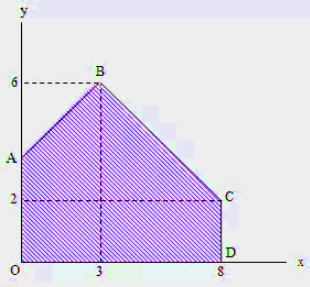Contoh Soal Program Linear

Pembahasan 2:

Titik ekstrim pada gambar ialah:

  • A tidak mungkin maksimum karena titik A paling kiri.
  • B(3, 6)
  • C(8, 2)
  • D(8, 0)

Nilai tiap titik ekstrim ialah:

  • B (3,6) → ƒ (3,6) = 4 (3) +5(6) =42
  • C (8,2) →ƒ (8,2) = 4(8) + 5(0) = 42
  • D (8,0) → ƒ ( 8.0) = 4(8) + 5 (0) =32

Sehingga dapat diketahui hasilnya bahwa nilai maksimumnya berada pada titik yang melalui garis BC dengan nilai maksimum 42.

DAFTAR PUSTAKA 

judul materi : PROGRAM LINEAR 

sumber materi : wirahadie (https://wirahadie.com/materi-matematika-kelas-11-bab-2/amp/), kabarkan.com (https://kabarkan.com/program-linear/)

tahun penerbitan sumber materi : wirahadie (2021), kabarkan.com (2022)



Komentar

Posting Komentar

Postingan populer dari blog ini

BARISAN DAN DERET

Gambar
A) barisan dan deret aritmatika Barisan dan deret ini tidak bisa dipisahkan karena memiliki keterkaitan satu sama lainnya. Sederhananya, barisan artimetika adalah bilangan dengan pola yang tetap berdasarkan operasi penjumlahan dan pengurangan. Sementara itu, deret aritmetika adalah jumlah n suku pertama barisan aritmetika. Aritmetika (kadang salah dieja sebagai aritmatika, berasal dari bahasa Yunani  αριθμός  –  arithmos  = angka) atau dulu disebut ilmu hitung merupakan cabang (atau pendahulu) matematika yang mempelajari  operasi  dasar bilangan. Oleh orang awam, kata “aritmetika” sering dianggap sebagai sinonim dari teori bilangan. Silakan lihat angka untuk mengetahui lebih dalam tentang teori bilangan. Barisan aritmetika ini dapat dinyatakan dengan rumus sebagai berikut. a a+b  a+2b a+3b Lebih lanjut, selisih antara nilai suku-suku saling berdekatan dan selalu sama, yaitu b. Misalnya: Un – U(n-1) = b Sebagai contoh baris 1, 3, 5, 7, 9, merupakan baris aritmetika dengan nilai: b = (9
Baca selengkapnya

turunan fungsi aljabar

Gambar
  Pengertian Turunan Fungsi Aljabar Turunan fungsi atau juga bisa disebut dengan diferensial adalah fungsi lain dari suatu fungsi sebelumnya, contohnya fungsi f dijadikan f' yang mempunyai nilai tidak memakai aturan dan hasil dari fungsi akan berubah sesuai dengan variabel yang dimasukan, atau secara umum suatu besaran yang berubah seiring perubahan besaran lainnya. Proses dalam menemukan turunan disebut sebagai diferensiasi. Lalu untuk pengertian turunan aljabar adalah perluasan dari materi limit fungsi. Notasi turunan fungsi aljabar seperti berikut: Seperti yang telah disebutkan di atas, jika turunan fungsi aljabar merupakan perluasan dari materi limit fungsi sehingga dapat didefinisikan seperti berikut: Rumus Turunan Aljabar Setelah memahami tentang pengertian dari turunan fungsi aljabar, hal yang perlu Sobat Pintar pelajari adalah rumus dari turunan fungsi aljabar. Rumus turunan fungsi aljabar ini terbagi menjadi beberapa rumus berikut: Turunan Fungsi Pangkat Turunan Hasil Kali
Baca selengkapnya

integrasi fungsi aljabar

Gambar
Apa Itu Integral Tak Tentu? Integral merupakan anti turunan atau kebalikan dari turunan yang berfungsi untuk menentukan daerah, volume, titik pusat, dan lainnya.  Kalau suatu fungsi f(x) dibalik menjadi f’(x) maka itu merupakan turunan. Nah, jika f’(x) dibalik lagi menjadi f(x), maka itu merupakan integral.  Sebelum ke rumus integral tak tentu, elo perlu paham konsep turunan nih. Gue kasih bayangin dikit tentang turunan secara umum. y= X3   Turunan dari soal ini berapa? dydx = 3×2  Setelah diturunkan seperti ini, lalu dikali silang. dy = 3×2 dx  d(X3) = 3×2 dx  Bisa dilihat ya, y diganti dengan X3 Nah, dari sini bisa kita simpulkan ya cara mencari turunan bentuknya akan seperti ini nih. Turunan dari X2 akan menjadi d(X2) = 2x dx Oke, konsep turunan udah ingat lanjut ke materi integral tak tentu lagi. Coba deh elo perhatikan antara turunan dan integral di bawah ini. Turunan: Sekarang kita balik, dikalikan silang ya: df(x) = f’(x)dx Kita tambahkan aja lambang integral (∫), menjadi: ∫df(x
Baca selengkapnya